Закон паскаля реферат, Uudelleenohjausilmoitus
Это происходит не только потому, что высота столба воздуха над ним уменьшается, но еще и потому, что уменьшается плотность воздуха. К г. Принять участие быстро, просто и удобно!
Исходя из этого я поставил следующие задачи: 1 Изучить литературу по данной теме.

Задачи с ветвлением и их решение. Program vetvlenie; Var t: integer; Begin. Программирование на языке Турбо Паскаль И, наконец, слово end с точкой в последней строке говорит о том, что программа Паскаль практическое использование Электронные вычислительные машины решают сегодня самые разнообразные задачи — управляют Ветвление в Паскале Теперь поговорим об условиях. В программах на языке Паскаль условия представляют собой выражения, значением которых Повествовательное предложение, о котором можно сказать верно оно или нет называют высказыванием.
Например: Сегодня вторник. Гидравлические машины урок в VII классе 1. Актуализация знаний: давление в жидкостях, закон Паскаля входной тест. Изучение и усвоение нового материала слайд-шоу. Закрепление нового материала карточки с задачами.
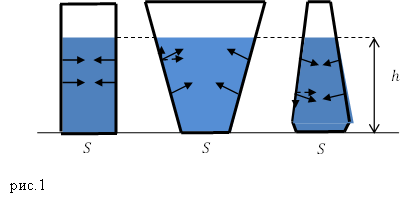
Ход урока: 1. Сегодня мы познакомимся с примером того, как Сила давления жидкости на дно сосуда в этом случае равна весу жидкости в сосуде.
Если же сосуд имеет наклонные стенки, давление жидкости на них имеет вертикальную составляющую. В расширяющемся кверху сосуде она направлена вниз, в сужающемся кверху сосуде она направлена вверх.
Вес жидкости в сосуде равен сумме вертикальных составляющих давления жидкости по всей внутренней площади сосуда, поэтому он и отличается от давления на дно [2].
В году парадокс продемонстрировал Блез Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кружку воды.
Из-за малого диаметра трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула. Похожий кажущийся парадокс возникает при рассмотрении закона Архимеда.
Согласно распространённой формулировке закона Архимеда , на погружённое в воду тело действует выталкивающая сила, равная весу воды, вытесненной этим телом. Из такой формулировки можно сделать неверное умозаключение, что тело не сможет плавать в сосуде, не содержащем достаточное количество воды для вытеснения.
Однако на практике тело может плавать в резервуаре с таким количеством воды, масса которой меньше массы плавающего тела. Это возможно в ситуации, когда резервуар лишь ненамного превышает размеры тела. Например, когда корабль стоит в тесном доке, он остаётся на плаву точно так же, как в открытом океане, хотя масса воды между кораблём и стенками дока может быть меньше, чем масса корабля [3].
Объяснение парадокса заключается в том, что архимедова сила создаётся гидростатическим давлением, которое зависит не от веса воды, а только от высоты её столба.
Как в гидростатическом парадоксе на дно сосуда действует сила весового давления воды, которая может быть больше веса самой воды в сосуде, так и в вышеописанной ситуации давление воды на днище корабля может создавать выталкивающую силу, превышающую вес этой воды [4].